Specific learning disability in mathematics: a comprehensive review
Introduction
Mathematics (math) is not only the science of numbers, but also is used in everyday life from calculating time and distance, to handling money and analyzing data to make decisions in financial planning and insurance purchasing, and is essential in the STEM (science, technology, engineering and math) fields. Infants have an innate capacity for “numerosity” or the number of things. In early childhood, counting is learned to bridge this innate capacity to more advanced math abilities like arithmetic facts and concepts (1). Math is a core subject taught in primary and higher education, which builds a foundation of math skills for real life situations. Numeracy is the knowledge and skills required to effectively manage and respond to the mathematical demands of diverse situations (2), and is a necessary skill in both blue-collar and professional work places. Analyses in both the United Kingdom (UK) and United States (US) revealed that poor numeracy skills impacted employment opportunities and wages, even in the presence of adequate literacy skills (3,4). Hence, it is concerning to note that the Nation’s Report Card from the National Assessment of Educational Progress (NAEP) yielded poorer results for 4th, 8th and 12th graders in the US in 2015 compared to 2013 (5), and only 9% of US adults scored in the highest numeracy levels in a 23 country comparative study (6). This has led to recommendations in the US aimed at improving math education, around curricular content, learning processes, instructional practices and materials, assessment, and teacher education (7). New standards like the Common Core State Standards (CCSS) (currently adopted in 42 states, District of Columbia and four territories) are designed to be relevant to the real world, while preparing students for post-secondary education and careers (8).
Terminology utilized to describe children who have difficulties with math varies in the literature depending upon how the study populations are defined and what instruments are used. Generally speaking, the term mathematical difficulties refers to children whose poor mathematics achievement is caused by a variety of factors from poor instruction to environmental factors, and represents a broader construct than does the term math disability (MD). Children with mathematical difficulties have low average performance or poor performance in math, but not all children with mathematical difficulties will have MD, which is hypothesized to be due to an inherent weakness in mathematical cognition not attributable to sociocultural or environmental causes (9). The continuously changing diagnostic criteria and varying definitions between the educational and medical/mental health realms add an additional confounder between the two terms. Terms like dyscalculia and poor math achievement add to the confusion as it is unclear if the terms are meant to be synonymous or overlapping (10). For the purposes of this review, the terms math learning disorder, math learning disability and dyscalculia will be considered as synonymous and represented by MD.
In many international clinical settings, criteria for MD is outlined in the World Health Organization International Statistical Classification of Diseases and Related Health Problems 10th edition (ICD-10). It is defined as a specific impairment in arithmetical skills not solely explicable on the basis of general mental retardation or of inadequate schooling, which involves mastery of basic computational skills rather than more abstract mathematical skills (11). For the US, the definition in the most recent revision of the Diagnostic and Statistical Manual of Mental Disorders (DSM) 5th edition, DSM-5 (12) is in the single category of specific learning disorders with specifiers for the area of math (others being reading and written expression). The definition states that difficulties should have persisted for at least six months despite interventions, and skills should be substantially below those expected for age. Deficits should interfere with functioning, as confirmed by individually administered standardized achievement measures and comprehensive clinical assessment. It includes possible deficits in number sense, memorization of math facts, calculation, and math reasoning.
Across reviews of studies (13), and as a matter of clinical practicality, most MD is identified by the school systems (educational and school psychologists, special educators among others). As such, it is critical to understand the changing criteria for MD determinations in the education system. With passage of the original version of Individuals with Disabilities Education Act (IDEA) in 1975 when specific learning disabilities (SLD) was recognized as a disability category for special education services, the operational definition was based on ability-achievement discrepancy in 1977 (14). Over time, the discrepancy model was deemed flawed and lacking in validity, and in 2004 reauthorization changed the definition to be based upon inadequate response to research based interventions (15). Yet, reviews of research indicate that despite the abandonment of the discrepancy model, studies continue to use this to identify subjects. Furthermore, much of the research on MD appears to be focused on elementary school children and basic math skills due to an emphasis on early identification and doesn’t pay adequate attention to MD in older children (16) where math involves complex domains like algebra, and math reasoning.
Prevalence
There are almost 2.5 million students (5%) with SLD receiving special education services in US public schools, but this number has declined in the last decade, largely due to increased use of instructional strategies, shifts in SLD identification and attention to early childhood education (17). There is a wide range of prevalence data in the research, depending on criteria used for identification and cut-offs for determination, as well as the country of study. Prevalence data has varied from 3–7% (12). With regards to gender, results have varied depending upon the criteria used for identification, and overall gender differences were not identified when using absolute thresholds or relative discrepancy criteria in defining MD (18-21).
Neurobiological basis
MD is considered a neurodevelopmental disorder, involving dysfunction in specific brain regions that are implicated in math skills. Numerosity is considered the building block of math skills, and relies on visual and auditory association cortices and the parietal attention system, specifically the intraparietal sulcus (IPS) within the posterior parietal cortex (PPC) (22). There is a developmental sequence in childhood to math acquisition; children initially rely on procedure-based counting (which when repeated, results in associations for retrieval). This is reflected in greater activation in functional imaging studies of the dorsal basal ganglia, which is involved in working memory (WM) (23). Gradual development shift mostly occurs in second and third grades to retrieval from long term memory, laying the foundation for more complex math skills (24). Brain involvement for complex math is based in the medial temporal lobe, with connections to other brain areas, especially the hippocampus and the prefrontal cortex (PFC). Younger children exhibit greater involvement of the hippocampus, and parahippocampal gyrus (25,26) compared to adults. The greater activation seen in this region in younger subjects may reflect the greater recruitment of processing resources for memorization and may also reflect novelty effects (27). As children mature, there is greater activation in the left PPC and lateral occipital temporal cortex along with lower activation in multiple PFC areas evincing more specialization (27).
Individuals with MD have reduced activation during math tasks in functional imaging studies involving the IPS (28,29) and structural imaging also showed reduced gray matter in the IPS in those with MD (30) and reduced connectivity between parietal and occipito-temporal regions (31). A recent study postulated that deficient fiber projection in the superior longitudinal fasciculus (particularly adjacent to the IPS) which connects parietal, temporal and frontal regions in children with MD is related to MD via a “disconnection” or interruption of integration and control of distributed brain processes (32). Since research in MD is not as established as reading disorders (RD) and is ongoing, no single hypothesis accounts for all children with MD. Multiple theories exist as described below.
Core deficit hypothesis
This predicts using neuro-imaging data that numeric concepts such as quantity, magnitude, numerosity are associated with the IPS. This is further distinguished as deficit in processing number magnitude (33) or deficit in number sense (34). However, developmental literature is inconclusive and inconsistent as MD has a complex and heterogenous clinical presentation (35).
Deficits in general domain hypothesis
This presumes there are subtypes of MD based on impairment in underlying cognitive processes. Three subtypes are thought to be associated, deficits in; verbal WM (necessary to acquire math procedures), long-term memory (necessary for storage and retrieval of math facts), and visuospatial processing (36).
Deficits in domain-specific math areas
The Triple Code model (37) of number processing hypothesizes there are three math domains: (I) numerical quantity representation (similar to number sense); (II) visuospatial numerical representation associated with attentional shifting; and (III) auditory verbally representation (associated with math facts and retrieval). This has some neuroanatomical support with IPS corresponding to first, posterior superior parietal lobule to second, and angular gyrus (AG) and perisylvian areas to the third domain respectively.
Procedural deficit hypothesis
This states that MD is a deficit of procedural memory involving a neural network of frontal, parietal, basal ganglia and cerebellar systems involved in storage and recall of skills. After practice, learned information is processed rapidly and automatically (38). However, while promising, it does not account for all cases of MD.
Genetic basis
There are thought to be a variety of intrinsic genetic contributors to MD, including genetic mutations and polymorphisms with hypothesized influences ranging from alterations in neural development to connectivity to epigenetic effects (39). Population-level studies take into account genetic variants on genotyping platforms and provide a lower bound estimate of heritability, while twin models capture all genetic factors and produce higher estimates due to the presence of dominance or interaction effects (40). Studies revealed that monozygotic and dizygotic twins of individuals with MD were twelve and eight times more likely to have MD, respectively (41) and >50% of siblings of individuals with MD also had MD (42). Math ability is thought to be influenced by many genes generating small effects across the entire spectrum of ability in genome-wide association studies (43) and around half of the observed correlation between math and reading ability is due to shared genetic effects (40). In a twin study, 60% of the genetic factors that influenced math ability also influenced reading ability and about 95% of the phenotypic correlation between the two is explained by these shared genetic influences (44).
Certain genetic conditions increase the risk of MD. Children with 22q11.2 deletion syndrome have deficits in calculation, math word problem solving and numerical quantities despite intact math fact retrieval (45). Children with Turner syndrome have intact number comprehension and processing skills, but have slower and more error-prone functioning on complex math problems (46). Children with fragile X syndrome have both MD and RD (47), while children with myelomeningocele have deficits in simple math, counting and math word problem solving despite relative strengths of basic number knowledge and language skills (48). Children with neurofibromatosis-1 have deficits in math calculation and math word problems and more variability in math skills than other genetic condition (49), and children with Williams syndrome have significant visuospatial deficits which may be responsible for their MD features (50).
Clinical presentation
While the theories described above are tested against cognitive neuroscience models, from a clinical perspective, it is helpful to classify presentations depending on the skills and deficits demonstrated. One such model from Karagiannakis et al. (51) has 4 subtypes of skills:
- Core number: which involves numerosity, estimating numbers and quantities, number line ability, managing symbols and basic counting;
- Memory: retrieving math facts, performing calculations, remembering rules and formulae;
- Reasoning: grasping math concepts, complex math procedures, logical problems and problem solving;
- Visuospatial: geometry, written calculations, graphs and tables.
Typically developing children may have an experiential knowledge of math even prior to formal school math education, where they get exposed to math facts and calculation procedures. Clinical features of a child presenting with MD (Table 1) largely depends on three factors: the age/developmental age of the child, the existing math instruction and curriculum exposure, and the presence of comorbid conditions.

Full table
The coexistence of another condition along with the primary condition under study is considered “comorbidity” (52). For MD, the most prevalent comorbidity is RD, with rates as high as 70%, and correspondingly for children with RD, rates of MD can be as high as 56% (18,53,54). The rates tend to be lower when more stringent cut-offs are applied to the definitions of the various disorders (55), and when population samples are studied compared to identified SLD samples. Distinguishing MD from comorbid MD with RD has focused on performance on nonverbal and verbal tests with studies showing that students with RD (and MD + RD) experienced more difficulty with phonology; students with MD (and MD + RD) more difficulty with processing speed, nonverbal reasoning, and most mathematical performances (56). While there have been suggestions that inattention and poor planning associated with attention deficit hyperactivity disorder (ADHD) may be responsible, MD and ADHD are thought to be comorbid separate disorders that are independently transmitted in families (57). A Spanish study (58), which attempted to distinguish the cognitive profiles between ADHD and MD children, revealed that simultaneous processing was more predictive in the MD group while executive processes was predictive in ADHD group.
Math anxiety is specific to math and is a negative emotional reaction or state of discomfort involving math tasks (59). It is not a rare phenomenon and has been found in 4% of high school students in the UK (60). Children with MD can develop a negative attitude towards math in general, and avoidance of math activities associated with anxious feelings. Negative experiences with math teachers compounds the situation. Poor math achievement is strongly related to math anxiety, especially when children are expected to work rapidly towards a single correct response (61). There is debate whether math anxiety is a distinct entity from generalized anxiety, as some studies have shown correlation with measures of general anxiety (62) while other studies show measures of math anxiety correlate more with one another than with test anxiety or general anxiety (63). Math anxiety is thought to develop as young as first grade (64), and brain activity shows that math anxious children show increased amygdala activity (emotional regulation) with reduced activity in dorsolateral PFC and PPC (WM and numerical processing) (65).
Evaluation
Screening
This is the first step in a diagnostic process, and is usually conducted with the general student population to identify “at-risk” children (as early as kindergarten) who need to proceed to a formal diagnostic process. Gersten et al. (66) outlines common components included in screening batteries such as: magnitude comparison, strategic counting, retrieval of basic arithmetic facts, and (more recently) word problems and numeral recognition. Single proficiency screening measures, which are easy to administer quickly with large numbers of students, have comparable predictive validities to multiple proficiency screening measures that cover a wider range of mathematics proficiencies and skills. No single test score is found to be predictive, though performance on number line estimation (67) and reading numerals, number constancy, magnitude judgments of one-digit numbers, and mental addition of one-digit numbers (68) are most correlated with math achievement. Additionally, testing WM is recommended along with math-specific items (68).
In the UK, a computerized screener has been used (69). In the US, the Response to Intervention (RTI) model (70) recommends screenings on a school-wide basis at least twice yearly, using an objective tool and focused on critical math objectives for each grade level that are prescribed at the state level (or CCSS as applicable). Curriculum-based measurement (CBM) probes are empirically supported for screening (71) and for math generally is a single proficiency measure (digit computation). Health professionals’ role in screening generally involves providing anticipatory guidance on development and behavior and surveillance for “early warning signs” of MD (especially in pre-K children) of difficulty counting loud and struggling with number recognition and rhyming (72). Other roles include investigating and treating potential medical problems that can affect the patient’s ability to learn (73) while ruling out medical differential diagnoses for learning problems like seizures, anemia, thyroid disease, sensory deficits and elevated lead levels.
Diagnosis
The process of diagnosis of MD depends on the discipline of the clinician first encountered, what criteria are used, as well as local and regional regulations. In early grades (kindergarten and first grade), diagnostics probe for functioning on foundational skills like core number processing. This is reliant on exposure to, and interaction with, symbolic processing skills as well as language and spatial processing. As children get older, increasing abstract concepts are relied on for math processing, and deficits in these are used to make the diagnosis (74). Differences observed in young children may result from exposure to mathematics before formal schooling or from student performance on more formal mathematics in school (66). Diagnostics can occur either in a medical interdisciplinary or educational model depending on local and regional availability and access to such clinicians.
Specialists in interdisciplinary clinics (like Child Neurologists, Developmental-Behavioral Pediatricians, Pediatric Psychologists) can be involved, often at the request of caregivers with referrals from primary care providers, or for independent consultations in event of questions or concerns about the adequacy of school services. This may engender tension between educators and medical professionals despite the acknowledged importance of collaboration; particularly around the perception that medical clinicians foster dissension between parents and schools, don’t acknowledge the competence of school personnel and make recommendations not reflecting the individual needs of the child or impact on the cost or structure of the child’s education (75). In the medical model, history is usually elicited around the child’s symptoms and current functioning in all academic areas, history of interventions or grade retention, family history of MD, presence of other developmental delays (gross, fine motor, visuomotor, language, adaptive) and behavioral symptoms (including anxiety, somatic symptoms and attentional issues). Apart from a physical and neurological examination, screening tests for learning disabilities are conducted. In the interdisciplinary team, clinical psychologists are invaluable in conducting diagnostic assessments including cognitive and academic batteries.
Neuropsychological testing (NPT) has been presumed to be broader than psychoeducational assessment and suggested as an essential part of SLD identification, as it can provide information on strengths and weaknesses, particularly if other medical conditions exist (76). While studies (77,78) have shown that performance on neuropsychological-psychological batteries can predict academic achievement later, such testing is time intensive and many insurances (both public and private) only consider NPT medically necessary in the assessment of cognitive impairment due to medical or psychiatric conditions. They explicitly exclude coverage for educational reasons (unless a qualifying medical disorder is present like metabolic disorders, neurocutaneous disorders, traumatic brain injury) and suggest that testing be provided by school systems. NPT is of value in context of medical disorders or when function deterioration (due to neurological conditions) is not adequately explained by social-emotional or environmental factors (79). However, one limitation of NPT is that reports offer hypotheses about a child’s level of functioning that may not account for, or be relevant to, planning interventions within the school setting and is more of a snapshot than a progressively developing picture that school personnel are privy to (79). There is emerging interest that technology and biopsychosocial data, such as eye-tracking data in combination with number line estimation tasks, might be a promising tool in diagnosing MD in children (80).
In an educational model, prior to the 2004 reauthorization of IDEA, eligibility for determination as SLD (including math) rested on the ability—achievement discrepancy model which required assessment of cognitive and academic functioning and relied on formulae that determined cut-offs. However, since 2004, local education agencies were permitted to adopt criteria that could either be the discrepancy model or an alternate based in evidence-based science. One of the latter, the RTI model (70) changed eligibility to students who fail to respond to increasing hierarchy of data-driven interventions based on individual student problems. However, despite the law and subsequent regulations, there is no directive regarding magnitude of achievement and progress targets for struggling learners which continues to create varying identification practices (81).
Another approach emphasizes the role of strengths and weaknesses in cognitive processing measured by individually administered standardized tests. This patterns of strengths and weaknesses (PSW) approach needs additional empirical evidence to determine the robustness of this model as an alternate to existing procedures (82). There continues to be considerable variability in the state practices using identification techniques, with 34 states continuing to use the discrepancy model, and 10 states explicitly prohibiting its use. While 45 states provide guidance on RTI implementation, only 8 states exclusively use RTI models in LD identification, but with variability regarding how to implement models. Less than half of the states allow use of PSW models, but with little information regarding identification practices. Prior to 2004, only half of the states included math reasoning as an area for LD identification, and this has increased to all presently (83). School eligibility evaluations are conducted by credentialed special education teachers, licensed educational psychologists, or school psychologists.
Generally, an evaluation consists of history and review of records, followed by psychometric testing for academic skills, intellectual abilities, sometimes executive function (EF), socio-emotional and behavioral assessment including qualitative information, classroom observations and questionnaires from caregivers and teachers. For MD, the assessment includes whether the student has mastery of math skills compared to the state’s academic content standards despite appropriate instruction and if the impact of the disability entitles the student to specialized instruction to benefit. The school evaluators prioritize educational goals and place them in the context of the school, which is the child’s natural environment (79).
Management
Educational Interventions
Teaching individuals with MD creates unique challenges in regular education environments, as teachers often struggle to provide individualized attention due to large class sizes, limited resources and learners with different styles. The overall goal is building knowledge and skills to develop automaticity. With students with MD, many math processes never become “automatic,” and they need extra time to improve WM and extra work on cognitive functions (84). The co-teaching model, in which children with MD are taught in the general education classroom, involves a general education teacher delivering overall instructional content, and a second special education teacher designing and delivering more intensive interventions and learning strategies as needed. This model is built around inclusion, to foster positive interaction and behavior among students, and to foster professional development among educators, but it has been criticized for not detecting or differentiating students with MD early in their education (85).
While the adoption of CCSS standardizes the expected knowledge and abilities of students at a certain grade level, and allows an easier transition if students move between districts or states, some suggest that it also may cause children to fall further behind their peers, and leave gaps in important skills and general math understanding. It can create hardship for students with MD as well; since the time constraints and the expected amount of material that students are expected to master may lead to students with MD not getting enough procedural practice, and repetition of the basic concepts in order to be successful (86). Since CCSS is reading intensive, students with comorbid LD and MD struggle to a greater extent, and there are additional challenges transitioning from an older curriculum, and the lack of professional development educators receive during this transition (87).
The RTI model is a three tiered system is used for early identification (and intervention) of children who may be at risk of future educational failure. The typical representation is a pyramid (Figure 1) of larger numbers in a generalized education environment with progressively smaller groups receiving additional instructional supports and finally students needing intensive instruction similar to specialized education. The model has the benefit of creating accountability by encouraging and guiding practitioners to intervene earlier with the great number of children at risk of failure, and by introducing a more valid method to identify student with MD with progress monitoring and motivational strategies, particularly for students in Tier 2 and Tier 3 instruction (88). The impetus for RTI has been primarily for reading, with slower adoption for math, though programs have been slowly expanding over the past five to ten years. There has been debate about the value of investment in small-group intervention, whether interventions should be aligned with core curriculum, and which students are likely to benefit from intervention. Small group interventions have consistently improved students’ math performance on proximal measures, that is, difficult grade level content and sophisticated topics. However, the effect on distal measures, that is building a general capacity in math, is less clear (89).
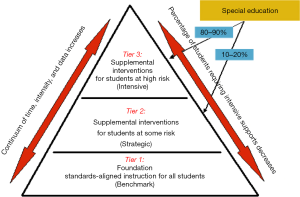
The National Center for Educational Evaluation and Regional Assistance recommends that instructional material should focus intensely on whole numbers in kindergarten through grade five, and on rational numbers in grades four through eight. Instruction should include at least ten minutes devoted to building fluent retrieval of facts, should be explicit and systematic, including providing models, verbalization of thought process, guided practice, corrective feedback, and frequent cumulative review, and students should have the opportunity to work with visual representations of mathematical ideas. Interestingly, in classrooms with a high percentage of students with MD, teachers are more likely to instruct with the use of manipulatives/calculators, or movement/music, or ordering and number/quantity skills, though these activities have not been associated with math achievement gains by students with MD. Students without MD benefit from both student-centered and teacher-directed activities. However, only increased classroom time doing teacher-directed activities is associated with positive gains in students with MD (90). One meta-analysis on teaching methods for children with MD revealed that students with lower math performance tend to respond better to instruction, and while interventions may help in many math domains, a smaller effect is seen in early numeracy and general math proficiency. Explicit teacher-led instruction, and peer-assisted learning have the largest affect, and providing instructional recommendations to teachers, and the use of technology may also have positive effects. Specific instructional components that may be beneficial for students with MD include controlling task difficulty, greater elaboration on topics, and working in a small group setting. Additionally, cognitive and metacognitive strategies computer-based interactive lessons, videos, and hands-on projects have been shown to aid math understanding and performance. Using concrete and visual representations along with teacher-facilitated instruction and virtual manipulatives have also been shown to be effective (91).
Three general strategies have been shown to be useful in accommodating children with MD including; improving reading skills, improving mathematical problem solving skills, and altering general instructional design (Table 2) (92). There are several specific math intervention programs which have gained research support. For a detailed description of these programs, see: http://www.hanoverresearch.com/2015/04/06/best-practices-in-math-interventions/. A detailed list of math interventions describing the appropriate age of learners and the level of evidence is also available at the What Works Clearinghouse, an online database created by the U.S Department of Education’s Institute of Education Sciences (93).

Full table
While emphasis is usually on implementing an intervention in the way it was researched and manualized, interventions are often slightly modified by special education teachers in response to their students’ notions of mathematics, and the particular need of individual students, or small groups of students. They do this through changing the pedagogy, materials, or tasks to bridge students’ prior and informal knowledge. They provide additional practice opportunities and connect procedural practices to larger concepts, provide additional time to practice in areas of difficulty, foster greater student interaction, and allow students more opportunity to think out loud and justify their thought processes (94). These practices should not be discouraged, because research has shown that training tailored to a child’s specific needs can create positive results (95).
Behavioral interventions
While educational interventions comprise the bulk of effective interventions for MD, there have been behavioral interventions that are effective in improving the math skills of children with MD, in the areas of EF, cognitive tutoring, and cognitive-behavior therapy (CBT) to improve performance, decrease math anxiety, and foster a positive attitude towards math.
EF broadly refers to the processes of attention, WM, long term planning, volition, and behavior inhibition (96) that allows students to organize and prioritize information, monitor progress, and adapt. Students who struggle with EF may have difficulty determining key information in math word problems, performing mental math, or starting a task, and they may make careless mistakes if they fail to check their work (97).
Strategies that can be implemented by school personnel include teaching positive self-regulatory skills through engagement, awareness of strengths and needs, goal setting, skill mastery, and generalization. A highly structured environment and schedule, limiting distractions, and providing interventional cues can foster self-regulation. For students who have difficulty with WM, teachers should limit the number of concepts presented at any one time, and may find it helpful to group information into chunks (97).
Improving attention in children with low arithmetical achievement may help to improve their abilities. Strategies include using instruction in improving reaction time, sensory (visual, auditory) selectivity, and attention shift (98). WM is specifically related to the ability of learn new math skills and is widely accepted to be impaired in individuals with MD. WM is correlated with math performance and is indicative of future math performance. WM training shows improvement in math skills especially when involving visuospatial WM (99). Cognitive tutoring has been found to be successful in improving math performance, effecting neuroplasticity, and changing the brain function of children with MD. Functional imaging studies have shown that initial differences in the prefrontal, parietal and ventral temporal-occipital cortices normalized after eight weeks of one-on-one tutoring focused on strengthening conceptual and procedural knowledge to support attention, WM, visuospatial skills, and cognitive inhibition necessary for math fluency (100).
Behavioral interventions are also important in addressing math anxiety, and early intervention is important as math anxiety tends to increase with age. Interventions include systematic desensitization, and cognitive behavior therapy (CBT); for example, expressive writing before a test may cause the student to reevaluate the need for worry, and therefore increase the WM available to perform specific tasks (101). Studies have shown that cognitive behavioral intervention with targeted tutoring may be helpful in decreasing anxiety, fostering a positive attitude towards math, and improving performance (102).
Novel approaches
Computer games and tutorials have been used for the past 30 years in special education to aid students with MD to improve basic math knowledge and skills (103). Rapid advances in broadband connectivity and ubiquity of mobile computing has led to almost every student having access to a computer connected to the internet, and increased digital content (104). Technology helps to emphasize important concepts, engage multiple sensory modalities, divide complex material into smaller components, and provide immediate feedback about accuracy (104). In one study, the use of math apps allowed both students with and without MD to make gains in math assessments. The larger gain was made in the struggling group, which helped to close the achievement gap (105).
Other technologies that can aid students with MD include computers and tablets with touch screens that are easier to use than traditional mouse and keyboards, and children can use them with little instruction (105). For students with MD, this type of feature allows for accommodations such as “talking calculators,” and the easy transfer of numbers to graphs, tables, and charts to create visual aids. Now, programs containing an artificial intelligence element can interactively tailor the features and settings of these programs, to the needs and abilities of particular students. For additional information about specific programs, please see the paper by Campuzano et al. (106).
Recent research has shown that virtual manipulatives can be invaluable when integrated with general math concepts to ensure a meaningful learning experience to match the individual student’s needs and abilities. For classrooms already equipped with computers, the cost is negligible since many virtual manipulative websites are easy to access, free of charge and don’t require storage or cleaning which benefits busy teachers (103). Video prompting using tablet devices have the added benefit of giving educators more time to work with small groups, or one-on-one, while others work in a self-directed manner, and students benefit by gaining independence, and becoming more accountable for their own learning (107).
Outcomes
The importance of identification and intervention is underscored by the impact of MD on child and adult functioning. Shalev et al. (108) demonstrated in a longitudinal study over three and six years that MD is persistent, which is similar to other developmental disorders like ADHD and RD with educational interventions not being protective against persistence of MD. There is limited research on SLD outcomes in adults, much less with respect to MD, and it tends to focus on young adulthood with limited data points which are less helpful about trends. The National Longitudinal Transition Study–2 only provides a snapshot of the immediate years after leaving school, lacks specific information about SLD in absence of other disabilities, and most information is about literacy and not numeracy. It also does not include persons who have dropped out of school, and describes attendance (but not completion) of two-year postsecondary schools. It does not track the types of employment and job advancement (109). Educational achievement is hypothesized to translate to higher SES through higher attained qualifications, improving occupational status and career development opportunities (110) and numeracy is associated with successful financial decision making (111).
Conclusions
Changing diagnostic manuals, different hypotheses regarding the core precepts of the disorder, and different criteria adopted in medical and educational systems can lead to different perspectives on MD. Advances in neuroscience and genetics offer promise in etiological determinations and understanding the neural processes underpinning MD. Clinical presentation varies depending on age and developmental status of the child, presence of other comorbid conditions, and the degree and nature of instructional methods used. The core interventions for MD continue to be educational in nature, with a varying degree of evidence-base that continues to grow. Additional avenues include behavioral interventions, which are primarily for comorbid conditions and math anxiety. Exciting new directions utilizing informational technology can help supplement educational interventions.
Acknowledgements
None.
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
References
- Butterworth B. The development of arithmetical abilities. J Child Psychol Psychiatry 2005;46:3-18. [Crossref] [PubMed]
- PIAAC Numeracy Expert Group. PIAAC numeracy: a conceptual framework, No. 35. Paris; 2009.
- Parsons S, Bynner J, Brewer E. Does numeracy matter more? Natl Res Dev Cent Adult Lit Numer 2005;1-37.
- Rivera-Batiz FL. Quantitative literacy and the likelihood of employment among young adults in the United States. J Hum Resour 1992;27:313-28. [Crossref]
- National Assessment of Educational Progress 2015 Mathematics Assessment: the nation’s report card. Washington DC; 2015.
- Goodman M, Finnegan R, Mohadjer L, et al. Literacy, numeracy, and problem solving in technology—rich environments among U.S. adults: results from the program for the international assessment of adult competencies 2012. Available online: https://nces.ed.gov/pubs2014/2014008.pdf
- Foundations for Success: The final report of the national mathematics advisory panel. Washington, DC; 2008.
- National Governors Association Center for Best Practices, Council of Chief State School Officers. Common core state standards for mathematics. 2010. Available online: http://www.corestandards.org/
- Mazzocco MM. Defining and differentiating mathematical learning disabilities and difficulties. In: Berch D, Mazzocco MM, editors. Why Is Math So Hard for Some Children? The Nature and Origins of Mathematical Learning Difficulties and Disabilities. Baltimore, MD: Paul H. Brookes Pub Co, 2007:29-47.
- Mazzocco MM. Challenges in identifying target skills for math disability screening and intervention. J Learn Disabil 2005;38:318-23. [Crossref] [PubMed]
- World Health Organization. International statistical classification of diseases and related health problems. 10th ed. Geneva.
- Specific Learning Disorder. In: Diagnostic and Statistical Manual of Mental Disorders. 5th ed. Washington, DC: American Psychiatric Association, 2013.
- Williams JL, Miciak J, McFarland L, et al. Learning disability identification criteria and reporting in empirical research: a review of 2001-2013. Learn Disabil Res Pract 2016;31:221-9. [Crossref]
- U.S. Office of Education. Assistance to states for education for handicapped children: Procedures for evaluating specific learning disabilities Federal Register, 42. Washington, DC; 1977.
- Individuals with Disabilities Education Improvement Act. 20 USC 1414(b)(6) 2004.
- Lewis KE, Fisher MB. Taking stock of 40 years of research on mathematical learning disability: methodological issues and future directions. J Res Math Educ 2016;47:338-71. [Crossref]
- Cortiella C, Horowitz SH. The state of learning disabilities: facts, trends and emerging issues. New York, NY; 2014.
- Dirks E, Spyer G, van Lieshout EC, et al. Prevalence of combined reading and arithmetic disabilities. J Learn Disabil 2008;41:460-73. [Crossref] [PubMed]
- Lewis C, Hitch GJ, Walker P. The prevalence of specific arithmetic difficulties and specific reading difficulties in 9- to 10-year-old boys and girls. J Child Psychol Psychiatry 1994;35:283-92. [Crossref] [PubMed]
- Devine A, Soltész F, Nobes A, et al. Gender differences in developmental dyscalculia depend on diagnostic criteria. Learn Instr 2013;27:31-9. [Crossref] [PubMed]
- Moll K, Kunze S, Neuhoff N, et al. Specific learning disorder: Prevalence and gender differences. PLoS One 2014;9:e103537. [Crossref] [PubMed]
- Dehaene S, Piazza M, Pinel P, et al. Three parietal circuits for number processing. Cogn Neuropsychol 2003;20:487-506. [Crossref] [PubMed]
- Chang C, Crottaz-Herbette S, Menon V. Temporal dynamics of basal ganglia response and connectivity during verbal working memory. Neuroimage 2007;34:1253-69. [Crossref] [PubMed]
- Menon V. A neurodevelopmental perspective on the role of memory systems in children’s math learning. In: Berch D, Geary D, Koepke KM, editors. Development of Mathematical Cognition vol. 2: Neural Substrates and Genetic Influences. Elsevier Inc 2016:79-107.
- Eichenbaum H. Hippocampus: mapping or memory? Curr Biol 2000;10:R785-7. [Crossref] [PubMed]
- De Smedt B, Holloway ID, Ansari D. Effects of problem size and arithmetic operation on brain activation during calculation in children with varying levels of arithmetical fluency. Neuroimage 2011;57:771-81. [Crossref] [PubMed]
- Menon V. Developmental cognitive neuroscience of arithmetic: implications for learning and education. ZDM 2010;42:515-25. [Crossref] [PubMed]
- Mussolin C, De Volder A, Grandin C, et al. Neural correlates of symbolic number comparison in developmental dyscalculia. J Cogn Neurosci 2010;22:860-74. [Crossref] [PubMed]
- Kucian K, Loenneker T, Dietrich T, et al. Impaired neural networks for approximate calculation in dyscalculic children: a functional MRI study. Behav Brain Funct 2006;2:31. [Crossref] [PubMed]
- Rotzer S, Kucian K, Martin E, et al. Optimized voxel-based morphometry in children with developmental dyscalculia. Neuroimage 2008;39:417-22. [Crossref] [PubMed]
- Rykhlevskaia E, Uddin LQ, Kondos L, et al. Neuroanatomical correlates of developmental dyscalculia: combined evidence from morphometry and tractography. Front Hum Neurosci 2009;3:51. [Crossref] [PubMed]
- Kucian K, Ashkenazi SS, Hänggi J, et al. Developmental dyscalculia: a dysconnection syndrome? Brain Struct Funct 2014;219:1721-33. [PubMed]
- Landerl K, Bevan A, Butterworth B. Developmental dyscalculia and basic numerical capacities: a study of 8-9-year-old students. Cognition. 2004;93:99-125. [Crossref] [PubMed]
- Robinson CS, Menchetti BM, Torgesen JK. Toward a Two-Factor Theory of One Type of Mathematics Disabilities. Learn Disabil Res Pract 2002;17:81-9. [Crossref]
- Moeller K, Fischer U, Cress U, et al. Diagnostics and intervention in developmental dyscalculia: current issues and novel perspectives. In: Breznitz Z, Rubinsten O, Molfese VJ. editors. Reading, Writing, Mathematics and the Developing Brain: Listening to Many Voices. Dordrecht: Springer Netherlands, 2012:233-75.
- Geary DC. Mathematics and learning disabilities. J Learn Disabil 2004;37:4-15. [Crossref] [PubMed]
- Wilson A, Dehaene S. Number sense and developmental dyscalculia: In Human behavior, learning, and the developing brain. In: Coch D, Dawson G, Fischer K, editors. Human behavior, learning, and the developing brain: Atypical development. New York: Guilford, 2007:212-38.
- Evans TM, Ullman MT. An extension of the procedural deficit hypothesis from developmental language disorders to mathematical disability. Front Psychol 2016;7:1318. [Crossref] [PubMed]
- Dennis M, Berch DB, Mazzocco MM. Mathematical learning disabilities in special populations: Phenotypic variation and cross-disorder comparisons. Dev Disabil Res Rev 2009;15:80-9. [Crossref] [PubMed]
- Davis OS, Band G, Pirinen M, et al. The correlation between reading and mathematics ability at age twelve has a substantial genetic component. Nat Commun 2014;5:4204. [Crossref] [PubMed]
- Alarcón M, DeFries JC, Light JG, et al. A twin study of mathematics disability. J Learn Disabil 1997;30:617-23. [Crossref] [PubMed]
- Shalev RS, Manor O, Kerem B, et al. Developmental dyscalculia is a familial learning disability. J Learn Disabil 2001;34:59-65. [Crossref] [PubMed]
- Docherty SJ, Davis OS, Kovas Y, et al. A genome-wide association study identifies multiple loci associated with mathematics ability and disability. Genes Brain Behav 2010;9:234-47. [Crossref] [PubMed]
- Markowitz EM, Willemsen G, Trumbetta SL, et al. The etiology of mathematical and reading (dis)ability covariation in a sample of Dutch twins. Twin Res Hum Genet 2005;8:585-93. [Crossref] [PubMed]
- De Smedt B, Swillen A, Verschaffel L, et al. Mathematical learning disabilities in children with 22q11.2 deletion syndrome: a review. Dev Disabil Res Rev 2009;15:4-10. [Crossref] [PubMed]
- Mazzocco MM. Mathematical learning disability in girls with Turner syndrome: a challenge to defining MLD and its subtypes. Dev Disabil Res Rev 2009;15:35-44. [Crossref] [PubMed]
- Murphy MM. A review of mathematical learning disabilities in children with fragile X syndrome. Dev Disabil Res Rev 2009;15:21-7. [Crossref] [PubMed]
- English LH, Barnes MA, Taylor HB, et al. Mathematical development in spina bifida. Dev Disabil Res Rev 2009;15:28-34. [Crossref] [PubMed]
- Moore BD. Potential influences on mathematical difficulties in children and adolescents with Neurofibromatosis, type 1. Dev Disabil Res Rev 2009;15:45-51. [Crossref] [PubMed]
- O'Hearn K, Luna B. Mathematical skills in Williams syndrome: insight into the importance of underlying representations. Dev Disabil Res Rev 2009;15:11-20. [Crossref] [PubMed]
- Karagiannakis G, Baccaglini-Frank A, Papadatos Y. Mathematical learning difficulties subtypes classification. Front Hum Neurosci 2014;8:57. [Crossref] [PubMed]
- Feinstein AR. The pre-therapeutic classification of co-morbidity in chronic disease. J Chronic Dis 1970;23:455-68. [Crossref] [PubMed]
- Barbaresi WJ, Katusic SK, Colligan RC, et al. Math learning disorder: Incidence in a population-based birth cohort, 1976-82, Rochester, Minn. Ambul Pediatr 2005;5:281-9. [Crossref] [PubMed]
- von Aster MG, Shalev RS. Number development and developmental dyscalculia. Dev Med Child Neurol 2007;49:868-73. [Crossref] [PubMed]
- Landerl K, Moll K. Comorbidity of learning disorders: prevalence and familial transmission. J Child Psychol Psychiatry 2010;51:287-94. [Crossref] [PubMed]
- Cirino PT, Fuchs LS, Elias JT, et al. Cogntive and mathematical profiles for different forms of learning difficulties. J Learn Disabil 2015;48:156-75. [Crossref] [PubMed]
- Monuteaux MC, Faraone SV, Herzig K, et al. ADHD and dyscalculia: evidence for independent familial transmission. J Learn Disabil 2005;38:86-93. [Crossref] [PubMed]
- Iglesias-Sarmiento V, Deaño M, Alfonso S, et al. Mathematical learning disabilities and attention deficit and/or hyperactivity disorder: A study of the cognitive processes involved in arithmetic problem solving. Res Dev Disabil 2017;61:44-54. [Crossref] [PubMed]
- Hembree R. The nature, effects, and relief of mathematics anxiety. J Res Math Educ 1990;21:33-46. [Crossref]
- Chinn S. Mathematics anxiety in secondary students in England. Dyslexia. 2009;15:61-8. [Crossref] [PubMed]
- Rubinsten O, Tannock R. Mathematics anxiety in children with developmental dyscalculia. Behav Brain Funct 2010;6:46. [Crossref] [PubMed]
- Wang Z, Hart SA, Kovas Y, et al. Who is afraid of math? Two sources of genetic variance for mathematical anxiety. J Child Psychol Psychiatry 2014;55:1056-64. [Crossref] [PubMed]
- Ashcraft MH, Krause JA. Working memory, math performance, and math anxiety. Psychon Bull Rev 2007;14:243-8. [Crossref] [PubMed]
- Maloney EA, Beilock SL. Math anxiety: who has it, why it develops, and how to guard against it. Trends Cogn Sci 2012;16:404-6. [Crossref] [PubMed]
- Young CB, Wu SS, Menon V. The neurodevelopmental basis of math anxiety. Psychol Sci 2012;23:492-501. [Crossref] [PubMed]
- Gersten RM, Clarke B, Jordan NC. Screening for mathematics difficulties in K-3 students. Portsmouth, NH 2007.
- Siegler RS, Booth JL. Development of numerical estimation in young children. Child Dev 2004;75:428-44. [Crossref] [PubMed]
- Mazzocco MM, Thompson RE. Kindergarten predictors of math learning disability. Learn Disabil Res Pract 2005;20:142-55. [Crossref] [PubMed]
- Butterworth B. Dyscalculia Screener. London: nferNelson Publishing Company Limited, 2003.
- Fuchs LS, Fuchs D, Compton DL, et al. Mathematics screening and progress monitoring at first grade: Implications for responsiveness to intervention. Except Child 2007;73:311-30. [Crossref]
- VanDerHeyden AM, Witt JC, Gilbertson D. A multi-year evaluation of the effects of a Response to Intervention (RTI) model on identification of children for special education. J Sch Psychol 2007;45:225-56. [Crossref]
- Council on early childhood, Council on school health. The pediatricians role in optimizing school readiness. Pediatrics 2016;138:e20162293. [Crossref] [PubMed]
- Bravender T. School performance: the pediatrician's role. Clin Pediatr (Phila) 2008;47:535-45. [Crossref] [PubMed]
- McLean JF, Rusconi E. Mathematical difficulties as decoupling of expectation and developmental trajectories. Front Hum Neurosci 2014;8:44. [Crossref] [PubMed]
- von Hahn L, Linse C, Hafler J. Hospital assessments of children with learning problems: perspectives from special education administrators and hospital evaluators. Ambul Pediatr 2002;2:11-6. [Crossref] [PubMed]
- Silver CH, Ruff RM, Iverson GL, et al. Learning disabilities: The need for neuropsychological evaluation. Arch Clin Neuropsychol 2008;23:217-9. [Crossref] [PubMed]
- Clarren SB, Martin DC, Townes BD. Academic achievement over a decade: A neuropsychological prediction study. Dev Neuropsychol 1993;9:161-76. [Crossref]
- Fayol M, Barrouillet P, Marinthe C. Predicting arithmetical achievement from neuro-psychological performance: a longitudinal study. Cognition 1998;68:B63-70. [Crossref] [PubMed]
- Sassu KA, Gelbar NW, Bray MA, et al. Exploring neuropsychology : seeking evidence of added worth to school psychology practice. School Psychology Forum 2015;9:269-76.
- van Viersen S, Slot EM, Kroesbergen EH, et al. The added value of eye-tracking in diagnosing dyscalculia: A case study. Front Psychol 2013;4:679. [Crossref] [PubMed]
- Zumeta RO, Zirkel PA, Danielson L. Identifying specific learning disabilities legislation, regulation, and court decisions. Top Lang Disord 2014;34:8-24. [Crossref]
- McGill RJ, Styck KM, Palomares RS, et al. Critical Issues in Specific Learning Disability Identification: What We Need to Know About the PSW Model. Learn Disabil Q 2016;39:159-70. [Crossref]
- Maki KE, Floyd RG, Roberson T, et al. State learning disability eligibility criteria: A comprehensive review. Sch Psychol Q 2015;30:457-69. [Crossref] [PubMed]
- Cawley J, Parmar R, Foley TE, et al. Arithmetic performance of students: implications for standards and programming. Except Child 2001;67:311-28. [Crossref]
- Scruggs TE, Mastropieri MA, McDuffie KA. Co-teaching in inclusive classrooms: A metasynthesis of qualitative research. Except Child 2007;73:392-416. [Crossref]
- Powell SR, Fuchs LS, Fuchs D. Reaching the mountaintop: Addressing the common core standards in mathematics for students with mathematics difficulties. Learn Disabil Res Pract 2013;28:38-48. [Crossref]
- Mills AR. Emergent themes surrounding the implementation of the common core state standards for mathematics for students with learning disabilities in mathematics. Northern Michigan University; 2015.
- Burton DT, Kappenberg J. Response to intervention: the teachers' role in distinguishing between mathematics difficulty and mathematics disability. Insights Learn Disabil 2010;7:53-64.
- Gersten R. What we are learning about mathematics interventions and conducting research on mathematics interventions. J Res Educ Eff 2016;9:684-8. [Crossref]
- Morgan PL, Farkas G, Maczuga S. Which instructional practices most help first-grade students with and without mathematics difficulties? Educ Eval Policy Anal 2015;37:184-205. [Crossref] [PubMed]
- Dennis MS, Sharp E, Chovanes J, et al. A meta-analysis of empirical research on teaching students with mathematics learning difficulties. Learn Disabil Res Pract 2016;31:156-68. [Crossref]
- Michaelson MT. An overview of dyscalculia: methods for ascertaining and accommodating dyscalculic children in the classroom. Aust Math Teach 2007;63:17-23.
- What works clearinghouse. Available online: https://ies.ed.gov/ncee/wwc/
- Hunt JH, Valentine C, Bryant DP, et al. Supplemental mathematics intervention: how and why special educators intensify intervention for students with learning disabilities. Remedial Spec Educ 2016;37:78-88. [Crossref]
- Re AM, Pedron M, Tressoldi PE, et al. Response to specific training for students with different levels of mathematical difficulties. Except Child 2014;80:337-52. [Crossref]
- Diamond A. Executive Functions. Annu Rev Psychol 2013;64:135-68. [Crossref] [PubMed]
- Watson MR, Gable RA, Morin LL. The role of executive functions in classroom instruction of students with learning disabilities. Int J Sch Cog Psychol 2016;3:167. [Crossref]
- Guarnera M, D’Amico A. Training of Attention in Children With Low Arithmetical Achievement. Eur J Psychol 2014;10:277-90. [Crossref]
- Bergman-Nutley S, Klingberg T. Effect of working memory training on working memory, arithmetic and following instructions. Psychol Res 2014;78:869-77. [Crossref] [PubMed]
- Iuculano T, Rosenberg-Lee M, Richardson J, et al. Cognitive tutoring induces widespread neuroplasticity and remediates brain function in children with mathematical learning disabilities. Nat Commun 2015;6:8453. [Crossref] [PubMed]
- Dowker A, Sarkar A, Looi CY. Mathematics anxiety: what have we learned in 60 years? Front Psychol 2016;7:508. [Crossref] [PubMed]
- Sokolowski HM, Necka EA. Remediating math anxiety through cognitive training: potential roles for math ability and social context. J Neurosci 2016;36:1439-41. [Crossref] [PubMed]
- Shin M, Bryant DP, Bryant BR, et al. Virtual manipulatives. Interv Sch Clin 2017;52:148-53. [Crossref]
- Lewandowski L, Wood W, Miller LA. Technological applications for individuals with learning disabilities and ADHD. In: Luiselli J, Fischer A. editors. Computer-Assisted and Web-based Innovations in Psychology, Special Education, and Health. Elsevier 2016:61-93.
- Zhang M, Trussell RP, Gallegos B, et al. Using math apps for improving student learning: an exploratory study in an inclusive fourth grade classroom. TechTrends 2015;59:32-9. [Crossref]
- Campuzano L, Dynarski M, Agodini R, et al. Effectiveness of reading and mathematics software products: findings from two student cohorts. NCEE 2009-4041. Natl Cent Educ Eval Reg Assist 2009.
- Edwards SE. Using video prompting to teach math skills to adolescent students with specific learning disabilities (SLD) via iPad. Brigham Young University–Provo 2015.
- Shalev RS, Manor O, Auerbach J, et al. Persistence of developmental dyscalculia: what counts? Results from a 3-year prospective follow-up study. J Pediatr 1998;133:358-62. [Crossref] [PubMed]
- Gerber PJ. The impact of learning disabilities on adulthood: a review of the evidenced-based literature for research and practice in adult education. J Learn Disabil 2012;45:31-46. [Crossref] [PubMed]
- Ritchie SJ, Bates TC. Enduring links from childhood mathematics and reading achievement to adult socioeconomic status. Psychol Sci 2013;24:1301-8. [Crossref] [PubMed]
- Agarwal S, Mazumder B. Cognitive abilities and household financial decision making. Am Econ J Appl Econ 2013;5:193-207. [Crossref]


